Calculus 3

12.1: Three-Dimensional Coordinate Systems

Distance Formula for 3-Dimensions

$$
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
$$
Derivation: Pythagorean Theorem

Equation of a Sphere

Center, $C(h, k, l)$ and radius, $r$
$$
(x-h)^2 + (y-k)^2 + (z-l)^2 = r^2
$$

Exercises

12.1 Problem 9

Find the lengths of the side of the triangle $PQR$. Is it a right triangle? Is it an isosceles triangle?

$P(3, -2, -3), \ Q(7, 0, 1),\ R(1, 2, 1)$
$$
s_1 = PQ = \sqrt{(x_p - x_q)^2 + (y_p - y_q)^2 + (z_p - z_q)^2} = \sqrt{4^2 + 2^2 + 4^2} = \sqrt{36} = 6
$$
$$
s_2 = QR = \sqrt{(x_q - x_r)^2 + (y_q - y_r)^2 + (z_q - z_r)^2} = \sqrt{6^2 + 2^2 + 0^2} = \sqrt{40} = 2\sqrt{10}
$$
$$
s_3 = PR = \sqrt{(x_p - x_r)^2 + (y_p - y_r)^2 + (z_p - z_r)^2} = \sqrt{2^2 + 4^2 + 4^2} = \sqrt{36} = 6
$$
Isosceles Triangle
Not a right triangle since $6^2 + 6^2 \neq 40$ (sides are not a pythagorean triplet)

12.1 Problem 13

Find an equation of the sphere with center (-3, 2, 5) and radius 4. What is the intersection of this sphere with the $yz$-plane?
$$
(x-h)^2 + (y-k)^2 + (z-l)^2 = r^2
$$
$$
(x+3)^2 + (y-2)^2 + (z-5)^2 = 4^2
$$
$$
(x+3)^2 + (y-2)^2 + (z-5)^2 = 16
$$

The intersection with the $yz$-plane will yield a circle.

Let $r_2$ be the radius of the circle created from the intersection.

Showing how to calculate r_2

$$
r_2 = \sqrt{4^2 - 3^2} = \sqrt{7}
$$

Thus the equation of the intersecting circle is
$$
(z - 5)^2 + (y-2)^2 = r_2^2
$$
$$
(z - 5)^2 + (y-2)^2 = 7
$$

12.1 Problem 15

Find an equation of the sphere that passes through the point (4, 3, -1) and has center (3, 8, 1)
$$
r = d = \sqrt{(4-3)^2 + (3-8)^2 + (-1 - 1)^2} = \sqrt{1 + 25 + 4} = \sqrt{30}
$$
$$
r^2 = (x-3)^2 + (y-8)^2 + (z - 1)^2 = 30
$$

12.2: Vectors

Vector: Quantity with both magnitude and direction (denoted v or $\vec{v}$ and graphically as an arrow)

Initial Point indicated by the “tail” of the arrow and the ending point is represented by the “head” of the arrow

Combining Vectors

$\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}$
The Triangle Law and Parallelogram Law are just ways of geometrically representing vector addition.
Scalar Multiplication: If $c$ is a scalar and $v$ is a vector, then cv is just the vector, $v$ with length multiplied by $|c|$. If $v = 0$, then $cv = 0$
Multiplying a vector by -1 means flipping the direction of the vector
$u - v = u + (-v)$

Components

If a vector, $a$ starts at the origin, then the coordinates are either $(a_1, a_2)$ or $(a_1, a_2, a_3)$ (2d vs. 3d)
These coordinates are called the components of $a$ and denoted with $\ev{a_1, a_2}$ or $\ev{a_1, a_2, a_3}$
Given the points $A(x_1, y_1, z_1)$ and $B(x_2, y_2, z_2)$, the vector $\textbf{a}$ with representation $\overrightarrow{AB}$ is
$$ \textbf{a} = \ev{x_2 - x_1, y_2 - y_1, z_2 - z_1}$$
The magnitude/length of the vector $\textbf{v}$ is the following:
$$ |\textbf{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$$

Properties of Vectors

$\textbf{a + b = b + a}$
$\textbf{a + 0 = a}$
$c(\textbf{a + b}) = c\textbf{a} + c\textbf{b}$
$(cd)\textbf{a} = c(d\textbf{a})$
$\textbf{a + (b + c) = (a + b) + c}$
$\textbf{a + (-a) = 0}$
$(c + d)\textbf{a} = c\textbf{a} + d\textbf{a}$
$1\textbf{a = a}$

Standard Basis Vectors and Unit Vectors

$$ \textbf{i} = \ev{1, 0, 0}$$
$$ \textbf{j} = \ev{0, 1, 0}$$
$$ \textbf{k} = \ev{0, 0, 1}$$
$\textbf{i}$, $\textbf{j}$, and $\textbf{k}$ are Standard Basis Vectors which point in the direction of the x, y, or z axis and have a length of 1

If a = $\ev{a_1, a_2, a_3}$, then a = $a_1 \textbf{i} + a_2 \textbf{j} + a_3 \textbf{k}$

Unit Vector: Vector with length 1 (So i, j, and k are examples of unit vectors)

If $a \neq 0$, then the unit vector with the same direction as a is
$$ \textbf{u} = \frac{\textbf{a}}{|\textbf{a}|} $$

Applications

Acceleration and Velocity
Force
- The resultant force or net force can be found by vector addition of the individual forces acting on an object

Exercises

Problem 2

What is the relationship between the point (4, 7) and the vector $\ev{4, 7}$? Illustrate with a sketch.

If the vector’s tail or starting point is located at the origin, then the head will be at the point (4, 7).

Problem 3

Name all the equal vectors in the parallelogram shown.

$$\overrightarrow{EA} = \overrightarrow{CE}\ \ \ \ \ \ \ \ \overrightarrow{DE} = \overrightarrow{EB}\ \ \ \ \ \ \ \ \overrightarrow{DA} = \overrightarrow{CB} \ \ \ \ \ \ \ \overrightarrow{AB} = \overrightarrow{DC}$$

Problem 4

Write each combination of vectors as a single vector.

a. $\overrightarrow{AC}$
b. $\overrightarrow{CB}$
c. $\overrightarrow{DB} - \overrightarrow{AB} = \overrightarrow{DB} + \overrightarrow{BA} = \overrightarrow{DA}$
d. $\overrightarrow{DC} + \overrightarrow{CA} + \overrightarrow{AB} = \overrightarrow{DA} + \overrightarrow{AB} = \overrightarrow{DB}$

Problem 6

Copy the vectors in the figure and use them to draw the following vectors.

Problem 7

In the figure, the tip of c and the tail of d are both the midpoint of $QR$. Express c and d in terms of a and b.

$$
c + d = b
$$
$$
c + (-d) = a
$$

$$
(c+d) + (c - d) = b+a
$$
$$
2c = b + a \implies c = \frac{b + a}{2}
$$

$$
\frac{b+a}{2} + d = b
$$
$$
d = b - \frac{b + a}{2} = \frac{2b - (b + a)}{2} = \frac{b - a}{2}
$$

Problem 8

If the vectors in the figure satisfy |u| = |v| = 1 and u + v + w = 0, what is |w|?

|w| = $\sqrt{2}$

Problem 9

Find a vector a with representation given by the directed line segment $\overrightarrow{AB}$. Draw $\overrightarrow{AB}$ and the equivalent representation starting at the origin.
$$ A(-2, 1), \ \ B(1, 2)$$
$$ \textbf{a} = \ev{1 - (-2), 2 - 1} = \ev{3, 1}$$

Problem 13

Find a vector a with representation given by the directed line segment $\overrightarrow{AB}$. Draw $\overrightarrow{AB}$ and the equivalent representation starting at the origin.
$$ A(0, 3, 1), \ \ B(2, 3, -1)$$
$$ \textbf{a} = \ev{2 - 0, 3 - 3, -1 - 1} = \ev{2, 0, -2}$$

Problem 15

Find the sum of the given vectors and illustrate geometrically.

$$ \ev{-1, 4}, \ \ \ev{6, -2}$$
$$ \ev{6 + (-1), -2 + 4} = \ev{5, 2}$$

Problem 17

Find the sum of the given vectors and illustrate geometrically.
$$ \ev{3, 0, 1}, \ \ \ev{0, 8, 0}$$
$$ \ev{3 + 0, 0 + 8, 1 + 0} = \ev{3, 8, 1}$$

Problem 19

Find a + b, 4a + 2b, |a|, and |a - b|.
a = $\ev{-3, 4}$, b = $\ev{9, -1}$

a + b =
$$\ev{-3 + 9, 4 + (-1)} = \ev{6, 3}$$

4a + 2b =
$$(4) \ev{-3, 4} + (2) \ev{9, -1}$$
$$ = \ev{-12, 16} + \ev{18, -2}= \ev{-12 + 18, 16 + (-2)}$$
$$ = \ev{6, 14}$$

|a| =
$$ \sqrt{(-3)^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 $$

a - b =
$$ \ev{-3, 4} - \ev{9, -1} = \ev{-3, 4} + \ev{-9, 1}$$
$$
\ev{-3 + -9, 4 + 1} = \ev{-12, 5}
$$

|a - b| =
$$ \sqrt{(-12)^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13 $$

Problem 21

Find a + b, 4a + 2b, |a|, and |a - b|.
a = $4\textbf{i} - 3\textbf{j} + 2\textbf{k}$, b = $2\textbf{i} - 4\textbf{k}$

a + b =
$$ (4 + 2)\textbf{i} + (-3 + 0)\textbf{j} + (2+ (-4))\textbf{k} = 6\textbf{i} -3\textbf{j} - 2\textbf{k} $$

4a + 2b =
$$
4(4\textbf{i} - 3\textbf{j} + 2\textbf{k}) + 2(2\textbf{i} - 4\textbf{k}) = (16\textbf{i} - 12\textbf{j} + 8\textbf{k}) + (4\textbf{i} - 8\textbf{k}) = 20\textbf{i} -12\textbf{j} + 0\textbf{k}
$$
$$
= 20\textbf{i} - 12\textbf{j}
$$

|a| =
$$
\sqrt{4^2 + (-3)^2 + (2)^2} = \sqrt{16 + 9 + 4} = \sqrt{29}
$$

a - b =

$$ (4 - 2)\textbf{i} + (-3 - 0)\textbf{j} + (2 - (-4))\textbf{k} = 2\textbf{i} -3\textbf{j} + 6\textbf{k} $$

|a - b| =
$$
\sqrt{2^2 + (-3)^2 + 6^2} = \sqrt{4 + 9 + 36} = \sqrt{49} = 7
$$

Problem 23

Find a unit vector that has the same direction as the given vector.
$$
\ev{6, -2}
$$
$$ \textbf{u} = \frac{\textbf{a}}{|\textbf{a}|} = \ev{6, -2} \frac{1}{\sqrt{6^2 + (-2)^2}} = \ev{6, -2} \frac{1}{\sqrt{40} } = \ev{6, -2} \frac{1}{2\sqrt{10}} $$
$$
= \ev{\frac{6}{2\sqrt{10}}, \frac{-2}{2\sqrt{10} }} = \ev{\frac{3}{\sqrt{10}}, -\frac{1}{\sqrt{10}}}
$$

Problem 25

Find a unit vector that has the same direction as the given vector.
$$
8\textbf{i} - \textbf{j} + 4\textbf{k}
$$
$$ \textbf{u} = \frac{\textbf{a}}{|\textbf{a}|} = (8\textbf{i} - \textbf{j} + 4\textbf{k} ) \frac{1}{\sqrt{8^2 + (-1)^2 + 4^2}} = (8\textbf{i} - \textbf{j} + 4\textbf{k} ) \frac{1}{\sqrt{64 + 1 + 16} } =(8\textbf{i} - \textbf{j} + 4\textbf{k} ) \frac{1}{\sqrt{81} } $$
$$
= (8\textbf{i} - \textbf{j} + 4\textbf{k} ) \frac{1}{9} = \frac{8}{9}\textbf{i} - \frac{1}{9}\textbf{j} + \frac{4}{9}\textbf{k}
$$

Problem 26

Find the vector that has the same direction as $\ev{6, 2, -3}$ but has length 4.

$$
\textbf{u} = \frac{\textbf{a}}{|\textbf{a}|} = \ev{6, 2, -3} \frac{1}{\sqrt{6^2 + 2^2 + (-3)^2}} = \ev{6, 2, -3} \frac{1}{36 + 4 + 9} = \ev{6, 2, -3} \frac{1}{\sqrt{49}} = \ev{\frac{6}{7}, \frac{2}{7}, -\frac{3}{7}}
$$
$$
4\textbf{u} = 4 \ev{\frac{6}{7}, \frac{2}{7}, -\frac{3}{7}} = \ev{\frac{24}{7}, \frac{8}{7}, -\frac{12}{7}}
$$

Problem 29

If v lies in the first quadrant and makes an angle $\frac{\pi}{3}$ with the positive $x$-axis and |v| = 4, find v in component form.

$$
\ev{4\cos{\frac{\pi}{3}}, 4\sin{\frac{\pi}{3}}} = \ev{\frac{4(1)}{2}, \frac{4 \sqrt{3} }{2}}
$$
$$
\ev{2, 2\sqrt{3}}
$$

Problem 43

If $A$, $B$, and $C$ are the vertices of a rectangle, find $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA}$

$$
\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} = \overrightarrow{AC} + \overrightarrow{CA} = \overrightarrow{AA} = 0
$$

Problem 44

Let $C$ be the point on the line segment $AB$ that is twice as far from $B$ as it is from $A$. If $\textbf{a} = \overrightarrow{OA}$, $\textbf{b} = \overrightarrow{OB}$, and $\textbf{c} = \overrightarrow{OC}$, show that $\textbf{c} = \frac{2}{3} \textbf{a} + \frac{1}{3}\textbf{b}$.

$$
-\textbf{a} = \overrightarrow{AO}
$$
$$
-a + b = \overrightarrow{AO} + \overrightarrow{OB} = \overrightarrow{AB}
$$
$$
\overrightarrow{AB} = \overrightarrow{AC} + \overrightarrow{CB} = \frac{1}{2}\overrightarrow{CB} + \overrightarrow{CB}
$$

$$
\overrightarrow{CO} + \overrightarrow{OB} = \overrightarrow{CB} = -\textbf{c} + \textbf{b}
$$

$$
\overrightarrow{AB} = \frac{1}{2}\overrightarrow{CB} + \overrightarrow{CB} = \frac{1}{2}(-c + b) + (-c + b)
$$

$$
(-a + b) = \frac{3}{2}(b - c)
$$
$$
\frac{2}{3}b - \frac{2}{3}a = b - c
$$

$$
\frac{2}{3}b - b - \frac{2}{3}a = -c
$$
$$
b - \frac{2}{3}b + \frac{2}{3}a = c
$$
$$
c = \frac{1}{3}b + \frac{2}{3}a
$$

Problem 45

a. Draw the vectors a = $\ev{3, 2}$, b = $\ev{2, -1}$, and c = $\ev{7, 1}$.

b. Show, by means of a sketch, that there are scalars $s$ and $t$ such that $\textbf{c} = s\textbf{a} + t\textbf{b}$.

Problem 47

If $\textbf{r} = \ev{x, y, z}$ and $\vb{r_0} = \ev{x_0, y_0, z_0}$, describe the set of all points $(x, y, z)$ such that $|\vb{r} - \vb{r_0}| = 1$.

$$
\vb{r} - \vb{r_0} = \ev{x - x_0, y-y_0, z-z_0}
$$
$$
|\vb{r} - \vb{r_0}| = \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2} = 1
$$
$$
(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 = 1^2
$$
The set of all points will form a sphere with center $(x_0, y_0, z_0)$ with a radius of $1$.

12.3: The Dot Product

If $\vb{a} = \ev{a_1, a_2, a_3}$ and $\vb{b} = \ev{b_1, b_2, b_3}$, then the dot product of $\vb{a}$ and $\vb{b}$ is denoted by $\vb{a} \cdot \vb{b}$ and is calculated by the following
$$ \vb{a} \cdot \vb{b} = a_1 b_1 + a_2 b_2 + a_3 b_3$$

The result of the dot product is a scalar quantity, not a vector.

Properties of the Dot Product

If $\vb{a}, \vb{b}, \vb{c}$ are vectors in $V_3$ and $c$ is a scalar, then

$\vb{a} \cdot \vb{a} = |\vb{a}|^2$
$\vb{a} \cdot \vb{b} = \vb{b} \cdot \vb{a}$
$\vb{a} \cdot (\vb{b} + \vb{c}) = \vb{a} \cdot \vb{b} + \vb{a} \cdot \vb{c}$
$(c\vb{a}) \cdot \vb{b} = c (\vb{a} \cdot \vb{b}) = \vb{a} \cdot (c\vb{b})$
$0 \cdot \vb{a} = 0$

If $\theta$ is the angle between the vectors $\vb{a}$ and $\vb{b}$, then
$$\vb{a} \cdot \vb{b} = |\vb{a}||\vb{b}|\cos\theta$$

Two vectors $\vb{a}$ and $\vb{b}$ are perpendicular/orthogonal iff $\vb{a} \cdot \vb{b} = 0$

Direction Angles and Direction Cosines

Direction Angles are the angles $\alpha, \beta, \gamma$ that $\vb{a}$ makes with the positive x-, y-, and z-axes, respectively.
$$ \vb{a} = |\vb{a}|\ev{\cos\alpha, \cos \beta, \cos\gamma}$$

Unit vector in direction of $\vb{a}$:
$$ u = \frac{1}{|\vb{a}|} \vb{a} = \ev{\cos \alpha, \cos \beta, \cos \gamma}$$

Projections

Vector Projection of $\vb{b}$ onto $\vb{a}$ is like the shadow of $\vb{b}$ in the direction of $\vb{a}$
The scalar projection of $\vb{b}$ onto $\vb{a}$ (also called the component of b along a) is defined to be the signed magnitude of the vector projection
$$ comp_a \vb{b} = \frac{\vb{a} \cdot \vb{b}}{|\vb{a}|} = |\vb{b}| \cos \theta$$
$$ proj_a \vb{b} = \left(\frac{\vb{a} \cdot \vb{b}}{|\vb{a}|}\right) \frac{\vb{a}}{|\vb{a}|} = \frac{\vb{a} \cdot \vb{b}}{|\vb{a}|^2} \vb{a}$$

$\theta$ is just the angle between the vectors.
The vector projection is the scalar projection times the unit vector in the direction of $\vb{a}$

Work

$W = \vb{F} \cdot \vb{d}$

12.4: The Cross Product

The Cross Product of $\vb{a}$ and $\vb{b}$ gives a vector that is perpendicular to both vectors (use right hand rule to find out direction of resultant vector)
If $\vb{a} = \ev{a_1, a_2, a_3}$ and $\vb{b} = \ev{b_1, b_2, b_3}$, then the cross product of $\vb{a}$ and $\vb{b}$ is the vector
$$ \vb{a} \times \vb{b} = \ev{a_2b_3 - a_3 b_2, a_3 b_1 - a_1b_3, a_1b_2, a_1b_2 - a_2 b_1} $$
Derivation: define a vector $\vb{c}$ that is perpendicular to both $\vb{a}$ and $\vb{b}$ such that the dot product is 0
Matrices can represent the above in a simpler fashion and less arbitrary looking way:

$$
\vb{a} \cross \vb{b} =
\begin{bmatrix}
\vb{i} & \vb{j} & \vb{k} \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3
\end{bmatrix} = \begin{bmatrix}
a_2 & a_3 \\
b_2 & b_3
\end{bmatrix} \vb{i} - \begin{bmatrix}
a_1 & a_3 \\
b_1 & b_3
\end{bmatrix} \vb{j} +
\begin{bmatrix}
a_1 & a_2 \\
b_1 & b_2
\end{bmatrix} \vb{k}
$$

Notice how the terms each have a unit vector and the determinant order 2 matrix is constructed from the original order 3 matrix with the row and column of the unit vector removed.
The determinant of order 2:
$$
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix} = ad - bc
$$
If $\theta$ is the angle between $\vb{a}$ and $\vb{b}$, then $|\vb{a} \cross \vb{b}| = |\vb{a} \mid \vb{b}| \sin\theta$
Two nonzero vectors $\vb{a}$ and $\vb{b}$ are parallel if and only if $\vb{a} \cross \vb{b} = 0$
The length of the cross product is equal to the area of the parallelogram formed by $\vb{a}$ and $\vb{b}$
The cross product is NOT commutative or associative

Properties of the Cross Product

$\vb{a} \cross \vb{b} = -\vb{b} \cross \vb{a}$
$(c\vb{a})\cross \vb{b} = c(\vb{a} \cross \vb{a}) = \vb{a} \cross (c\vb{b})$
$\vb{a} \cross (\vb{b} + \vb{c}) = \vb{a} \cross \vb{b} + \vb{a} \cross \vb{c}$
$(\vb{a} + \vb{b}) \cross \vb{c} = \vb{a} \cross \vb{c} + \vb{b} \cross \vb{c}$
$\vb{a} \cdot (\vb{b} \cross \vb{c}) = (\vb{a} \cross \vb{b}) \cdot \vb{c}$
$\vb{a} \cross (\vb{b} \cross \vb{c}) = (\vb{a} \cdot \vb{c}) \vb{b} - (\vb{a} \cdot \vb{b}) \vb{c}$

Triple Products

Scalar triple product (Property 5):
$$
\vb{a} \cdot (\vb{b} \cross \vb{c}) = \begin{bmatrix}
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3 \\
c_1 & c_2 & c_3
\end{bmatrix}
$$
The scalar triple product describes the volume of the parallelepiped
Vector triple product: Property 6

Torque

$|\vb{\tau}| = |\vb{r} \cross \vb{F}|$

12.5: Equations of Lines and Planes

Lines

$L$ is a line in 3d space. The vector equation of $L$ is the following
$$ \vb{r} = \vb{r_0} + t\vb{v}$$
where $t$ is a parameter, $\vb{r_0}$ is a position vector to a point on L, and $\vb{r}$ gives a point on L.

If $\vb{r} = \ev{x, y, z}$ and $\vb{r_0} = \ev{x_0, y_0, z_0}$,
the parametric equations for a line through the point ($x_0, y_0, z_0$) and parallel to the direction vector $\ev{a, b, c}$ are
$$ x = x_0 + at, \ \ \ y = y_0 + bt, \ \ \ z = z_0 + ct$$

Symmetric Equations of L:
$$ \frac{x-x_0}{a} = \frac{y-y_0}{b} = \frac{z-z_0}{c} $$
If $a$, $b$, or $c$ are 0:

Example: If $a = 0$, then $x_0 = x \ \ \ \ \frac{y-y_0}{b} = \frac{z-z_0}{c}$, and the line L lies in the vertical plane $x=x_0$

Line segment from $r_0$ to $r_1$:
$$ \vb{r}(t) = (1-t)\vb{r_0} + t\vb{r_1} \ \ \ \ 0 \le t \le 1 $$

Planes

Vector Equation of the Plane:
$$ \vb{n} \cdot (\vb{r} - \vb{r_0}) = 0$$
$$ \vb{n} \cdot \vb{r} = \vb{n} \cdot \vb{r_0}$$
$n$ is the normal vector (perpendicular to the plane)
$r_0$ and $r$ are position vectors
$r - r_0$ represent a line on the plane.

Scalar Equation of the Plane:
$$ a(x-x_0) + b(y-y_0) + c(z - z_0) = 0$$
where $\vb{n} = \ev{a, b, c}$ and point $P_0(x_0, y_0, z_0)$ is on the plane

Linear Equation Form of the Scalar Equation of a Plane
$$ ax + by + cz + d = 0$$
where $d = -(ax_0 + by_0 + cz_0)$

Two planes are parallel if their normal vectors are parallel.

Distances

$$ D = \frac{|ax_1 + by_1 + cz_1 + d|}{\sqrt{a^2 + b^2 + c^2}}$$
Derivation: The distance from an arbitrary point to a plane is the scalar projection of the distance between any point on the plane and the arbitrary point onto the normal vector.

12.6: Cylinders and Quadratic Surfaces

Traces/Cross Sections: Curves of intersections of surfaces with planes parallel to the coordinate planes
Steps for sketching surface:
- Find intercepts by settings two variables to zero and solving for third
- Make the “different” variable the axis that the surface is formed around (vertical axis) (e.g. all other variables on one side of equation or only one variable has negative)
- Determine the “traces” by holding one variable constant and seeing what the equation with two variables represents (hyperbola, parabola, or ellipse)

Cylinders

Cylinder: Surface with all lines (rulings) parallel to a given line and pass through a given plane curve.
Equation only has two variables (e.g. $x^2 + y^2 = 1$, $y^2 + z^2 = 1$
Example: $z = x^2$
Let $z$ be the vertical axis
If $y$ is set to be a constant, it doesn’t affect the equation and the traces formed by intersection with the xz plane will form parabolic cross sections since $z= x^2$ is a parabola when graphed on the x-z plane
If $z$ is held constant, you have $c = x^2$, where c is a constant. This equation is just two lines on the xy plane. So the traces formed from the intersection with the xz plane will form cross sections that consist of two lines.
If $x$ is held constant, you have $z = c$, where c is a constant. This is just the equation of one line on the yz plane.

Plot of function

Quadratic Surfaces

Equations have the form $Ax^2 + By^2 + Cz^2 + Dxy + Eyz + Fxz + Gx + Hy + Iz + J = 0$

Ellipsoid

All traces are ellipses
If $a = b= c$, the ellipsoid is a sphere
$\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1$

Plot of function

Elliptic Paraboloid

Horizontal traces (cross sections formed by intersection with xy plane) are ellipses
Vertical traces are parabolas
Axis of the parabola is the one that’s different (the one with degree one in the equation)
$\frac{z}{c} = \frac{x^2}{a^2} + \frac{y^2}{b^2}$

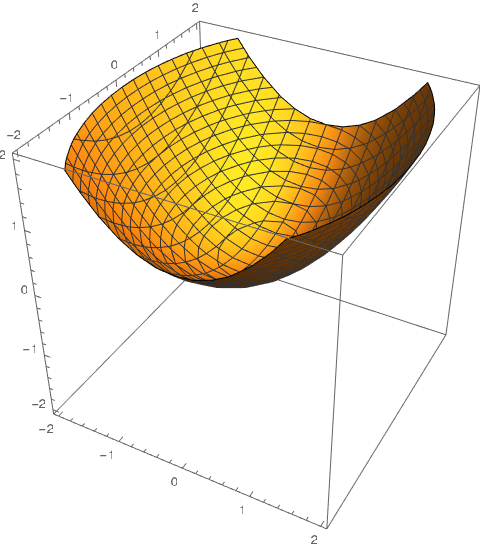
Plot of function

Hyperbolic Paraboloid

Horizontal traces (cross sections formed by intersection with planes parallel to the xy plane) are hyperbolas
Vertical traces (cross sections formed by intersection with planes parallel to the yz and xz planes) are parabolas
$\frac{z}{c} = \frac{x^2}{a^2} -\frac{y^2}{b^2}$

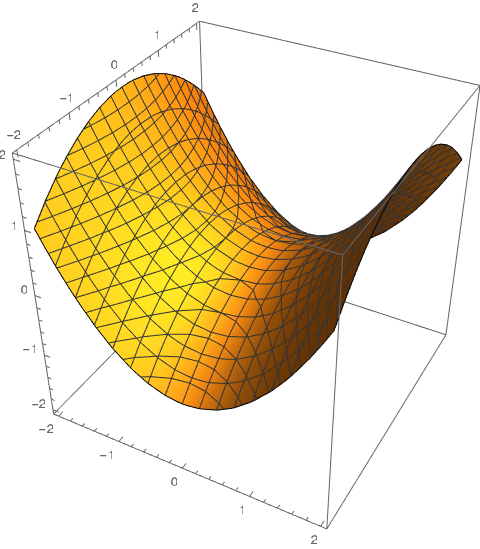
Plot of function

Cone

Horizontal traces are ellipses
Vertical traces are planes (except when x = 0 and y = 0 when the traces are a pair of lines)
$\frac{z^2}{c^2} = \frac{x^2}{a^2} + \frac{y^2}{b^2}$

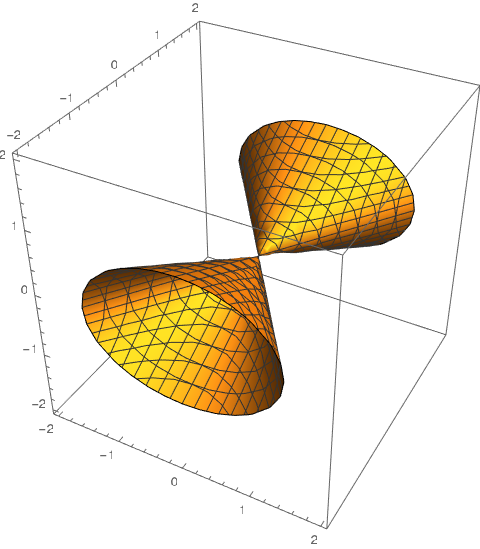
Plot of a function

Hyperboloid of One Sheets

Horizontal traces are ellipses
Vertical traces are hyperbolas
$\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1$

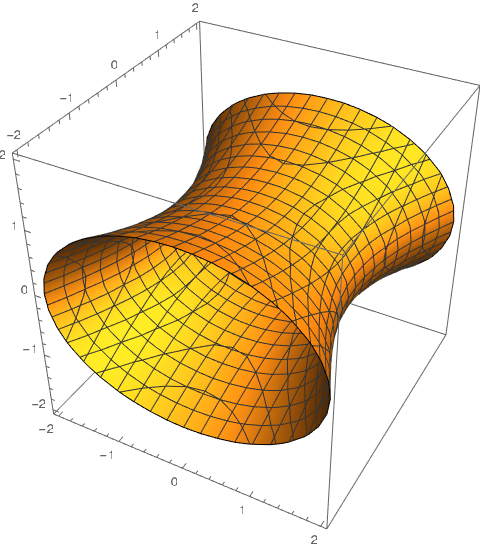
Plot of function

Hyperboloid of Two Sheets

Horizontal traces are ellipses if they exist
Vertical traces are hyperbolas
$-\frac{x^2}{a^2} - \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1$

Plot of function

13.1: Vector Functions and Space Curves

Vector Function: Domain: A set of real numbers, Range: A set of vectors

Let $\vb{r}$ be a vector function for 3-d vectors
The components of $\vb{r}$ are $f$, $g$, and $h$.
$$ \vb{r}(t) = \ev{f(t), g(t), h(t)} = f(t)\vb{i} + g(t) \vb{j} + h(t) \vb{k}$$

Limits and Continuity

$$\vb{r}(t) = \ev{f(t), g(t), h(t)}$$
$$ \lim_{t \to a} \vb{r}(t) = \ev{\lim_{t \to a} f(t), \lim_{t \to a} g(t), \lim_{t \to a} h(t)} $$
As long as the limits of the component functions exist.

$\vb{r}$ is continuous at $a$ if $\lim_{t\to a} \vb{r}(t) = \vb{r}(a)$

Space Curves

$C$ is the set of all points $(x, y, z)$ where $x = f(t), y = g(t), z = h(t)$ (Parametric equations of C with $t$ as the parameter)
Space Curve: The set of points in $C$
$C$ is traced out by the tip of the vector $\vb{r}(t)$

Drawing Curves

To sketch parametric equations, remove $t$ from the equation and get the equations in terms of the $x$, $y$, and $z$ instead
Then you can draw those equations on the x-y, y-z, and x-z planes. These “shadows” will represent the projections of the actual curve onto those planes.

13.2: Derivatives and Integrals of Vector Functions

$$
\frac{d \vb{r}}{dt} = \vb{r}'(t) = \lim_{h \to 0} \frac{\vb{r}(t+h) - \vb{r}(t)}{h}
$$
Unit Tangent Vector
$$
\vb{T}(t) = \frac{\vb{r}'(t)}{|\vb{r}'(t)|}
$$

If $f$, $g$, and $h$ are differentiable and $\vb{r}$ is a vector function
$$
\vb{r}'(t) = \ev{f’(t), g’(t), h’(t)}
$$

Differentiation Rules

$\frac{d}{dt}[\vb{u}(t) + \vb{v}(t)]=\vb{u}'(t) + \vb{v}'(t)$
$\frac{d}{dt}[ c\vb{u}(t)] = c\vb{u}'(t)$
$\frac{d}{dt}[f(t)\vb{u}(t)] = f’(t) \vb{u}(t) + f(t) \vb{u}'(t)$
$\frac{d}{dt}[ \vb{u}(t) \cdot \vb{v}(t)] =\vb{u}'(t) \cdot \vb{t} + \vb{u}(t) \cdot \vb{v} ‘(t)$
$\frac{d}{dt} [\vb{u}(t) \cross \vb{v}(t)] = \vb{u}'(t) \cross \vb{v}(t) + \vb{u}(t) \cross \vb{v}'(t)$
$\frac{d}{dt}[ \vb{u}f(t)] = f’(t)\vb{u}'(f(t))$

Integrals

$$
\int_{a}^{b} \vb{r}(t) dt = \left(\int_{a}^{b} f(t)dt\right) \vb{i} + \left(\int_a^b g(t)dt \right) \vb{j} + \left(\int_a^b h(t)dt\right)\vb{k}
$$

13.3: Arc Length and Curvature

Length of a Curve

$$ L = \int_a^b \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dx}{dt}\right)^2} dt= \int_{a}^{b} |\vb{r}'(t)| dt $$

Note that a space curve can be represented by different bu equivalent vector functions (e.g. $r(t) = \ev{t, t^2, t^3}$ is equivalent to $r(u) = \ev{e^u, e^{2u}, e^{3u}}$).
These different representations are called parameterizations of the curve and the arc length calculation does not change with the choice of parameterization.

The Arc Length Function

The arc length, $s$, can be defined calculated using the following:
$$ s(t) = \int_a^t \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dx}{dt}\right)^2} dt$$

Sometimes a curve is parametrized with respect to arc length which means redefining $r(t)$ in terms of $s$ instead of $t$.

Curvature

A curve is smooth on an interval if $r'$ is continuous and $r’(t) \neq 0$ on an interval.
Tangent unit vector, $T$:
$$ \vb{T}(t) = \frac{\vb{r}'(t)}{|\vb{r}'(t)|}$$

Curvature of a curve:
$$
\kappa = \left| \frac{d\vb{T}}{ds} \right|
$$
$$
\kappa (t) = \frac{|\vb{T}'(t)|}{|\vb{r}'(t)|} = \frac{|\vb{r}'(t) \cross \vb{r}''(t)|}{|\vb{r}'(t)|^3}
$$

Normal and Binormal Vectors

Unit Normal Vector: $\vb{N}(t)$ is a special vector that is orthogonal to $\vb{T}$ (indicates where curve is turning)
$$
\vb{N}(t) = \frac{\vb{T}'(t)}{|\vb{T}'(t)|}
$$
Note that $\vb{T}(t) \cdot \vb{T}'(t) = 0$, so the derivative of $\vb{T}$ is orthogonal to $\vb{T}$.
Binormal Vector: Also a unit vector but orthogonal to both $\vb{T}$ and $\vb{N}$
$$
\vb{B}(t) = \vb{T}(t) \cross \vb{N}(t)
$$
Normal Plane: Plane that contains $\vb{N}$ and $\vb{B}$. The plane contains all lines orthogonal to $\vb{T}$
Osculating Plane: Plane that contains $\vb{N}$ and $\vb{T}$. The plane is the plane that comes closest to containing the part of the curve near the point of the tangent.

13.4: Motion in Space: Velocity and Acceleration

Velocity Vector v(t):
$$ \vb{v}(t) = \lim_{h\to 0} \frac{\vb{r}(t+h) -\vb{r}(t)}{h} = \vb{r}'(t)$$

Speed:
$$ |\vb{v}(t)| = |\vb{r}'(t)| = \frac{ds}{dt} $$

Acceleration:
$$ \vb{a}(t) = \vb{v}'(t) = \vb{r}''(t)$$

Projectile Motion

Assuming Gravitational acceleration of, $g$ and no air resistance

$$ x = (v_0 \cos \alpha )t, \ \ \ \ y = (v_0 \sin \alpha ) t - \frac{1}{2} gt^2$$

Tangential and Normal Components of Acceleration

$$\vb{a} = v’\vb{T} + \kappa v^2 \vb{N}$$
$$a_T = v’ = \frac{\vb{v} \cdot \vb{a}}{v} = \frac{\vb{r}'(t) \cdot \vb{r}''(t)}{|\vb{r}'(t)|}$$
$$a_N = \kappa v^2 = \frac{|\vb{r}'(t) \cross \vb{r}''(t)}{|\vb{r}'(t)|}$$

14.1: Functions of Several Variables

Function of two variables: Assigns ordered pair $(x, y)$, in a set $D$ a unique real number. $D$ is the domain and the range is the set. The function is denoted by $z = f(x, y)$, where $x$ and $y$ are independent variables and $z$ is the dependent variable. For a function of two variables, the domain is a subset of $\mathbb{R}^2$ and the range is a subset of $\mathbb{R}$ (the range is always like this).

Domain and Range

A function can be visualized as a mapping between the domain and range, where each value in the domain only maps to one value in the range
When graphing the domain, the number of dimensions is equal to the number of independent variables
The range’s dimensions is always one

Graphs

Another way to visualize functions is by graphing
The number of dimensions required to graph a function is the number of independent variables + the number of dependent variables
- This means the dimensions of the graph of the functions is always independent variables + 1
For $z = f(x, y)$, the graph can thought of as a surface above or below the xy plane, where the domain is the xy plane

Level Curves (Contour Plots)

The third way to visualize functions is with contour plots also known as level curves
For functions of two variables, the level curves are the curves with equations
$$f(x, y) = k$$
where $k$ is a constant in the range of $f$.
Examples of contour plots are in topological maps that indicate how steep and high mountains or hills are
When level curves are closer together, the surface is “steeper”
For functions of two variables, the equation $f(x, y) = z = ax + by + c$ is called the linear function and represents a plane

14.3: Partial Derivatives

The $\textbf{partial derivative of } \mathbf{f} \textbf{ with respect to } \mathbf{x} \textbf{ at }\mathbf{(a, b)}$

$$ f_x(a, b) = g’(a) \ \ \text{where } g(x) = f(x, b)$$

$$ f_x(x, y) = \pdv{}{x} f(x, y) = \lim_{h\to 0} \frac{f(x+h, y) - f(x, y)}{h} $$
$$ f_y(x, y) = \pdv{}{y} f(x, y) = \lim_{h\to 0} \frac{f(x, y + h) - f(x, y)}{h} $$

To find the partial derivative with respect to $x$, hold $y$ constant
To find the partial derivative with respect to $y$, hold $x$ constant

Interpretations of Partial Derivatives

$$ z= f(x, y)$$

For the above function/surface, if we have a point $P(a, b, c)$, then when we hold $x$ constant with $x = a$, we get a curve, since the plane $x = a$ intersected with the surface, $f$
$g’(a) = f_x(a, b)$ represents the line tangent to the curve at that point.

Higher Derivatives

$$(f_{x})_{y} = f_{xy} = \pdv{}{y}\left(\pdv{f}{x}\right) = \pdv[2]{f}{y}{x}$$

Clairaut’s Theorem:
If $F$ is defined on a disk, $D$, that contains point $(a, b)$, and both $f_{xy}$ and $f_{yx}$ are continuous on the disk, then $f_{xy}(a, b) = f_{yx}(a, b)$

Partial Differential Equations

Partial Differential Equations: Used to express physical laws and describe phenomina
Laplace’s equation: The following partial differential equation (2 dimensional version):
$$ \pdv[2]{u}{x} + \pdv[2]{u}{y} = 0$$
Harmonic Functions: The solutions to Laplace’s equation
- Used in heat conduction, fluid flow, electric potential, etc
Wave Equation: Describes waves
$$ \pdv[2]{u}{t} = a^2 \pdv[2]{u}{x}$$

14.4: Tangent Planes and Linear Approximation

Tangent Planes

If $f$ has continuous partial derivatives, the equation of the tangent plane at a point is the following:
$$ z - z_0 = f_x(x_0, y_0) (x - x_0) + f_y(x_0, y_0)(y-y_0)$$

This is similar to how in single-variable calculus, the equation of the tangent line was the following:
$$ y-y_0 = f’(x_0)(x - x_0)$$

Linear Approximations

You can use the tangent plane at a point to approximate a function at a nearby point like in single-variable calculus.

14.5: Chain Rule

From single variable calculus
$$\frac{df}{dx}= \frac{d}{dx}\left(f(g(x))\right) = f’(g(x)) g’(x) = \frac{df}{dg}\frac{dg}{dx}$$

For multivariable:
$$ \frac{dw}{dt} = \frac{d}{dt} \left(x(t), y(t)\right) = \pdv{w}{x} \dv{x}{t} + \pdv{w}{y} \dv{y}{t}$$

14.6: Directional Derivative and Gradient

Directional Derivative

If $f$ is differentiable, $f$ has a directional derivative in the direction of the unit vector $\vb{u} = \ev{a, b}$
$$ D_u f(x, y) = f_x(x, y)a + f_y(x, y)b = \ev{f_x(x, y), f_y(x, y)} \cdot \vb{u}$$

Gradient vector

$$\nabla f = \text{del } f = \ev{f_x(x, y), f_y(x, y)}$$

Maximizing the Directional Derivative

Q. If we have a function $f$, and consider all directional derivatives at a point, then which directional derivative is greatest (“steepest” or has the fastest rate of change)
A. When $\vb{u}$ is in the same direction as the gradient vector since that will maximize the directional derivative

Equation of Tangent Plane to Level Surface

$$ \pdv{F}{x} \dv{x}{t} + \pdv{F}{y} \dv{y}{t} + \pdv{F}{z} \dv{z}{t} = 0$$
$$ \nabla F \cdot \vb{r}'(t) = 0$$
$$ F_x(x_0, y_0, z_0) (x-x_0) + F_y(x_0, y_0, z_0) (y - y_0) + F_z(x_0, y_0, z_0)(z-z_0)=0$$

14.7: Maximums and Minimums (Optimization)

$z=f(x, y)$ to be optimized

Local max at $(x_0, y_0)$ if $f(x, y) \le f(x_0, y_0)$ for all points $(x, y)$ near $(x_0, y_0)$

1st Derivative Test

Local extrema at $(a, b)$ if $\nabla f(a, b) = DNE$ or $\nabla f(a, b) = 0$ (Converse is not true)

2nd Derivative Test

Suppose $\nabla f(a, b) = \ev{0, 0}$

Calculate the following
$$D = det\left(\begin{bmatrix}
f_{xx} & f_{xy} \\
f_{yx} & f_{yy}
\end{bmatrix} \right) = f_{xx} f_{yy} - f_{xy}^2$$

If $D(a, b) < 0$, there is no local extrema, but there is a saddlepoint
If $D(a, b) = 0$, no conclusion is possible
If $D(a, b) > 0$, then calculate $f_{xx}$

If $f_x(a, b) > 0$, there is a local min
If $f_x(a, b) < 0$, there is a local max
If $f_x(a, b) = 0$, no conclusion is possible

15.1: Double Integrals over Rectangles

Volume $V$ of a solid above the rectangle $R$ and below the surface $z = f(x, y)$:
$$ V = \iint\limits_R f(x, y) dA $$
where $dA$ represents the area of the sub-rectangles that compose the large rectangle $R$.

Fubini’s Theorem

If $f$ is continuous on the rectangle $R = \{(x, y) | a \le x \le b, c\le y \le d \}$, then
$$ \iint\limits_R f(x, y) dA = \int_a^b \int_c^d f(x, y) \, dy \, dx = \int_d^c \int_a^b f(x, y) \, dx \, dy$$

If $R = [a, b] \cross [c, d]$
$$ \iint\limits_R g(x) \, h(y) \, dA = \int_a^b g(x) \, dx \int_c^d h(y) \, dy$$

15.2: Double Integrals over General Regions

We can take the double integral over a general region $D$ instead of just a rectangle
Let $F(x, y)$ be defined as the following:
$$
F(x, y) = \begin{cases}
f(x, y) & \text{if }(x, y) \text{ is in } D \\
0 & \text{if }(x, y) \text{ is in } R \text{ but not in } D
\end{cases}
$$

$$ \iint\limits_{D} f(x, y) dA = \iint\limits_R F(x, y) dA$$

If $D$ is lies between two continuous functions, $g_1(x)$, and $g_2(x)$ and if $f$ is continuous on a region $D$ such that
$$ D = \{ a \le x \le b, g_1(x) \le y \le g_2(x)\}$$
then
$$ \iint\limits_{D} f(x, y)\, dA = \int_a^b \int_{g_1(x)}^{g_2(x)} f(x, y) \, dy \, dx$$
If $f$ is continuous on a region $D$ such that
$$ D = \{ c \le y \le d, h_1(y) \le y \le h_2(y)\}$$
then
$$ \iint\limits_{D} f(x, y)\, dA = \int_b^c \int_{h_1(y)}^{h_2(y)} f(x, y) \, dx \, dy$$

Properties of Double Integrals

$$ \iint\limits_D \left(f(x, y) + g(x, y)\right) \, dA = \iint\limits_D f(x, y) \, dA + \iint_D g(x, y) \, dA $$
If $c$ is a constant, $$ \iint\limits_D cf(x, y) \, dA = c \iint\limits_D f(x, y) \, dA $$
If $f(x, y) \ge g(x, y)$ for all $x, y$ in $D$
$$ \iint\limits_D f(x, y) \, dA \ge \iint\limits_D g(x, y) \, dA $$
If $D = D_1 \cup D_2$, and $D_1$ and $D_2$ don’t overlap
$$ \iint\limits_D f(x, y)\, dA = \iint\limits_{D_1} f(x, y) \, dA + \iint\limits_{D_2} f(x, y) \, dA $$
$$ \iint\limits_D 1 \, dA = A(D) = \text{Area of }D$$
If $m \le f(x, y) \le M \; \forall (x, y) \in D$
$$ m \, A(D) \le \iint\limits_D f(x, y) \, dA \le M\,A(D)$$

15.3: Double Integrals in Polar Coordinates

$$ x = r \cos \theta \;\;\;\;\; y = r \sin \theta \;\;\;\;\; x^2 + y^2 = r^2$$

Double Integrals over Polar Rectangles

$$ \iint\limits_R f(x, y) \, dA = \int_{\alpha}^{\beta} \int_b^a f(r \cos \theta, \, r \sin \theta) r \, dr \,d\theta$$

Double Integrals over General Polar Regions

$$ \iint\limits_D f(x, y) \, dA = \int_{\alpha}^{\beta} \int_{h_1(\theta)}^{h_2(\theta)} f(r \cos \theta, \, r \sin \theta) r \, dr \,d\theta$$

15.5: Surface Area

For a function $f(x, y)$, the surface area can be computed with the following:
$$ A(S) = \iint\limits_D \sqrt{f_x(x, y)^2 + f_y(x, y)^2 + 1} \; dA$$

15.6: Triple Integrals

15.7: Triple Integrals with Cylindrical Coordinates

Cylindrical to rectangular
$$ x = r \cos \theta, \ \ \ y = r \sin \theta, \ \ \ z = z$$

Rectangular to Cylindrical
$$ r^2 = x^2 + y^2, \ \ \ \tan \theta = \frac{y}{x}, \ \ \ z = z$$

15.8: Triple Integrals with Spherical Coordinates

$$ x = \rho \sin \phi \cos \theta, \ \ \ y = \rho \sin \phi \sin \theta, \ \ \ z= \rho \cos \phi $$

$$ \rho^2 = x^2 + y^2 + z^2$$

$$ \iiint\limits_{E} f(x, y, z) \ dV= \int_c^d \int_\alpha^\beta \int_a^b f(\rho \sin \phi \cos \theta, \rho \sin \phi \sin \theta, \rho \cos \phi) \ \rho^2 \sin \phi \ d \rho \ d\phi \ d\theta $$

16.2: Line Integrals

Line Integrals of Functions

$C$ is a curve

$$ \int_{C} f(x, y) \ \ ds= \int_{a}^{b} f(x(t), y(t)) \ \ \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} \ \ dt$$

Line integrals of Vector Fields

Calculate a line integral along a curve $C$ in a vector field $\vec{F}$

$$ \int\limits_C \vec{F} \cdot d\vec{r} = \int\limits_C \vec{F} \cdot \vec{T} \ ds$$
where $\vec{T}$ is a unit tangent vector to $C$ in the direction of increasing $T$

Calculation (in general): use parametrization
$$ = \int_a^b \vec{F}\left( \vec{r}(t) \right) \cdot \vec{r}’ (t) \ dt $$

16.7: Surface Integrals (of Functions)

$S$ is a surface given by $z = f(x, y)$ where $(x, y) \in D$

$$ \iint\limits_S g(x, y, z) \ dS = \iint\limits_D g(x, y, f(x, y)) \sqrt{1 + f_x(x, y)^2 + f_y(x,y)^2} \ dA$$

For surface area, $g(x, y, z) = 1$

16.4: Green’s Theorem

To evaluate a line integral:
$$ \int_C \vec{F} \cdot d\vec{r}$$
Three options

From definition: use a parametrization $\vec{r}(t)$ for C, etc.
Use Fundamental Theorem: only works if $\vec{F}$ is conservative and needs a potential
Green’s Theorem: Needs C to be closed

Given

A curve $C$ (“piecewise smooth”) in $xy$-plane
- closed: start = end
- simple: does not cross itself (no figure 8)
- positively oriented (counterclockwise) - easy adjustment if clockwise
$D$ (region in the $xy$-plane
a vector field $\vec{F} = \ev{P(x, y), Q(x, y)}$

Green’s Theorem

$$ \int_C \vec{F} \cdot d\vec{r} = \iint\limits_{D} (Q_x - P_y) \ \ dA $$

Remarks

Green’s Theorem implies the criterion (earlier)
$$ \vec{F} \text{ conservative } \iff P_y = Q_x$$

Forward implication follows from Clairaut’s Theorem
Reverse implication follows from Green’s Theorem

Right Hand Side (RHS) is usually earlier than the LHS

Example

Evaluate $\oint x^2 y^2 \ dx + xy \ dy$

$C$: arc of the parabola $y=x^2$ from $(0,0)$ to $(1, 1)$ followed by the line segments $(1, 1)$ to $(0, 1)$ and from $(0,1)$ to $(0,0)$

$$ P = x^2 y^2, \ \ Q = xy $$

$$ P_y = 2yx^2, \ \ Q_x = y$$

$$ \int_C \vec{F} \cdot d\vec{r} = \iint\limits_D (y - 2yx^2) \ dA$$

$$ = \int_{0}^{1} \int_{x^2}^{1} (y - 2yx^2)\ dy \ dx$$
$$ = \int_0^1 \left. \frac{y^2}{2} - y^2 x^2 \right\vert_{y = x^2}^{y = 1} dx = \int_0^1 \left(-\frac{x^4}{2}+ x^4 + (\frac{1}{2} - x^2)\right) dx$$

Example

$$ \oint \vec{F} \cdot d\vec{r}$$
$$ \vec{F} = \ev{e^{-x} + y^2 , e^{-y} + x^2}$$
$C$: Arc of the curve $y = \cos x$ from $(-\frac{\pi}{2}, 0)$ to $(\frac{\pi}{2} , 0)$ followed by the line segment back from $(\frac{\pi}{2}, 0)$ to $(\frac{-\pi}{2}, 0)$

Clockwise!

Rule: For any curve $C$, $-C$ denotes $C$ with the direction reversed

Outlook

Green’s Theorem implies the earlier criterion: $P_y = Q_x \implies \vec{F} \text{ is conservative }$
$$ \int_C \vec{F} \cdot d\vec{r} = \iint_D \underbrace{0}_{Q_x - P_y = 0} dA = 0$$

for any closed, single curve (any orientation), $C$

It then follows that, for any curve $C$ (not necessarily closed), $\int_C \vec{F} \cdot d\vec{r}$ only depends on the end points of $C$

Independence of path

16.4: Curl and Divergence (n = 3)

3-dimensions

Given: $\vec{F} = \ev{P(x, y, z), Q(x, y, z), R(x, y, z)}$

Let $\nabla = \ev{\pdv{}{x}, \pdv{y}, \pdv{t}}$

then for a function $f = f(x, y, z)$
$\nabla f = \ev{\pdv{x} f, \pdv{y} f, \pdv{z} f}$ as we know already (gradient)

Definition

$$ div \vec{F} = \nabla \cdot \vec{F} = \pdv{x} P + \pdv{y} Q + \pdv{z} R =P_x + Q_y + R_z$$

$$ curl \vec{F} = \nabla \cross \vec{F} = \begin{bmatrix} \hat{i} & \hat{j} & \hat{k} \\ \pdv{x} & \pdv{y} & \pdv{z} \\ P & Q & R \end{bmatrix} = \ev{R_y - Q_z, P_z - R_x, Q_x - P_y}$$

Theorem

$$ \vec{F} \text{ conservative } \iff \curl\vec{F} = \ev{0, 0, 0}$$

Remarks

Generalizes our old criterion for conservativity of $\vec{F} = \ev{P(x, y), Q(x, y), 0}$
Again (as for n=2), the implication $\implies$ follows from Clairaut’s Theorem

$$ \vec{F} \text{ is conservative} \implies \exists f: \nabla f = \vec{F} \implies \curl \vec{F} = \nabla \cross \nabla f = \ev{0, 0, 0}$$

Example

$$\vec{F} = \ev{xyz^4, x^2 z^4, 4x^2 yz^3}$$

Is the above conservative?
If so, find a potential

$$ \nabla \cross \vec{F} = \ev{R_y - Q_z, P_z - R_x, Q_x - P_y} $$

$$ P_y = xz^4$$
$$ Q_x = 2xz^4$$

$xz^4 \neq 2xz^4$, so $\vec{F}$ is not conservative

Facts

$\vec{F}$ is conservative $\iff$ curl $\vec{F} = \vec{0}$
div(curl($\vec{F}$)) = 0

16.7: Surface Integrals (Of Vector Fields)

New: Surface Integrals of Vector Fields

Only for surfaces of the form
$$ S: z = g(x, y) \ \ \ \ (x, y) \in D$$

$$ \iint\limits_S \vec{F} \cdot d\vec{S} = \iint\limits_S \vec{F} \cdot \underbrace{\vec{n}}_{\text{unit normal vector}} \ dS $$

$$ = \iint\limits_D \vec{F} \cdot \vec{n} \sqrt{1 + g_x^2 + g_y^2} \ dA $$

Applications

“Flux” of $\vec{F}$ across the surface $S$

$> 0 $ means more gas flows through $S$ in the direction of $\vec{n}$ (upwards) than the opposite direction

In detail

Upward orientation
$$ \vec{n} = \frac{\ev{1, 0, g_x} \cross \ev{0, 1, g_y}}{|\ev{1, 0, g_x} \cross \ev{0, 1, g_y}|} = \frac{\ev{-g_x, -g_y, 1}}{\sqrt{1+g_x^2 + g_y^2}}$$

where $\ev{1, 0, g_x}$ and $\ev{0, 1, g_y}$ are tangent vectors to a point on $S$

Formula (For calculations)

Assuming $n$ is upwards (if downwards, then negate the formula for $n$)
$$ \vec{F} = \ev{P, Q, R}$$
$$ \vec{n} = \frac{\ev{-g_x, -g_y, 1}}{\sqrt{1+g_x^2 + g_y^2}}$$

$$ \iint\limits_{S} \vec{F} \cdot d\vec{S} = \iint\limits_D \vec{F} \cdot \vec{n} \sqrt{1 + g_x^2 + g_y^2} \ dA$$
$$ \iint\limits_{S} \vec{F} \cdot d\vec{S} = \iint\limits_D \vec{F} \cdot \ev{-g_x, -g_y, 1} \ dA= \iint\limits_D \left(-P \ g_{x} - Q \ g_{y} + R\right) \ dA$$

Example

$$ \vec{F} = \ev{-x, -y, z^3}$$

$S$: part of the cone $z = \sqrt{x^2 + y^2}$
between the surfaces $z = 1$ and $z = 3$
Orientation: Downwards

$$ g_x = \frac{x}{x^2 + y^2}$$
$$ g_y = \frac{y}{x^2 + y^2}$$

$$ \iint\limits_{S} \vec{F} \cdot d\vec{S} = - \iint\limits_D (-P g_x - Q g_y + R) \ dA$$
$$ = - \iint\limits_{D} \left(\frac{x^2}{\sqrt{x^2 + y^2}} + \frac{y^2}{\sqrt{x^2 + y^2}}\right) + (z^3) \ dA$$
$$ = -\iint\limits_{D} \left(\frac{x^2}{\sqrt{x^2 + y^2}} + \frac{y^2}{\sqrt{x^2 + y^2}}\right) + (x^2 + y^2)^{3/2} \ dA$$
$$ = - \int_{0}^{2\pi} \int_{1}^{3} (r^2 + r^4) \ dr \ d\theta = - \frac{1712}{15} \pi$$

Application: Net flow of gas is up since flux is negative and normal is down

16.8: Stokes’ Theorem

Calculates result for surface integral in a certain case

$$ \iint\limits_S (curl \ \vec{F}) \cdot d\vec{S} = \oint\limits_C \vec{F} \cdot d\vec{r}$$

$S$ is an oriented (up or down) surface in $\mathbb{R}^3$
$\vec{F} = \ev{P, Q, R}$
$C$: Closed curve that forms boundary of the surface $S$ in $\mathbb{R}^3$ oriented according to Right Hand Rule (RHR)

Special Case of Stokes’ Theorem

$$ \vec{F} = \ev{P, Q, 0}$$
$$ P= P(x, y) \ \ \ Q = Q(x, y)$$

$$ curl \ \vec{F} = \ev{0, 0, Q_x - P_y}$$

$$ (x, y) \in D$$

$$S = D \text{ in the xy plane} = \text{interior of curve }C$$

Stokes’ Theorem states:
$$ \oint\limits_C \vec{F} \cdot d\vec{r} = \iint\limits_D (Q_x - P_y) \ dA$$

Note that the above result is just Green’s Theorem
Stokes’ Theorem can be viewed as a general version of Green’s Theorem

Example

Calculate the following
$$ \iint\limits_S \left(curl \ \vec{F}\right) \cdot d \vec{S} $$

$$ \vec{F} = \ev{x^2 z^2 , yz^2, \tan^{-1} (x^2 yz^2)}$$
$$ S: z = \sqrt{x^2+y^2} \text{ cone oriented up} \ 0 \le z \le 2$$

Boundary curve $C$ (counter-clockwise by RHR)
$$ x^2 + y^2 = 4$$

Parametrization is still counter-clockwise
$$ C: \vec{r}(t) = \ev{ 2\cos t,2 \sin t, 2}$$

$$ \iint\limits_S (curl \ \vec{F})\cdot d\vec{S} = \oint\limits_C \vec{F} \cdot d\vec{r}$$
Just calculate line integral

16.9 Divergence Theorem (Dim 3)

Given

$\vec{F} = \ev{P, Q, R}$
$E$ as a solid in $\mathbb{R}^3$ (“simple” $\implies$ bounded)
$S = \partial E$ (boundary of $E$ oriented upwards)

$$ \iint\limits_{S} \vec{F} \cdot \vec{dS} = \iiint\limits_{E} div\ \vec{F} \ dV$$

Example

$$ \vec{F} = \ev{x^2 y z , xy^2 z, xyz^2}$$

S = the box enclosed by the following
$$ x= 0, x = a, y = 0, y=b, z = 0. z =c$$

Orientation is outwards

$$ \iint\limits_{S} \vec{F} \cdot \vec{dS} = \iiint\limits_{E} div \ \vec{F} \ dV$$
$$= \int_0^a \int_0^b \int_0^c div \ \vec{F} \ dz \ dy \ dx $$

$$= \int_0^a \int_0^b \int_0^c div \ \vec{F} \ dz \ dy \ dx = a^2b^2c^2 \div F $$

Example

$$ \vec{F} = \ev{z, y, zx}$$
S = surface of the tetrahedron enclosed by the coordinate planes & the plane
$$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$$

E = inside tetrahedron

$$ \iint\limits_{S} \vec{F} \cdot \vec{dS} = \iiint\limits_{E} div\ \vec{F} \ dV$$
$$\iiint\limits_{E} (1 +x) \ dV$$
$$ 0 \le x \le b$$
$$ 0 \le y \le b\left(1 - \frac{x}{a}\right)$$
$$ 0\le z \le c\left(1 - \frac{x}{a} - \frac{y}{b}\right)$$

$$ \int_0^{a} \int_{0}^{b(1-\frac{x}{a})} \int_0^{c(1-\frac{x}{a} - \frac{y}{b})} (1+x) dz \ dy \ dx$$

Summary of Green’s, Stokes’, Divergence Theorems

Green’s Theorem
$$ \vec{F} = \ev{P, Q}, \ \ \ P(x, y) = P, \ \ \ Q(x, y) = Q$$
$C$ closed curve in $xy$ plane ($\mathbb{R}$) oriented counter clockwise (positive orientation)
$$ \oint\limits_C = \vec{F} \cdot d\vec{r} = \iint\limits_D (Q_x - P_y) \ dA$$
where $D$=Interior of $C$
Stokes’ Theorem
$$ \vec{F} = \ev{P, Q, R}, \ \ \ P(x, y) = P, \ \ \ Q(x, y) = Q, \ \ \ R = R(x, y)$$
Closed curve $C$ in $\mathbb{R}^3$ oriented counter-clockwise when viewed from above

$$ \oint\limits_C \vec{F} \cdot d\vec{r} = \iint\limits_S \curl F \cdot d\vec{s}$$ where $S$ is a surface in $\mathbb{R}$ with boundary $C$ and $\vec{n}$ oriented up

Divergence Theorem
$F$ is the same as in Stokes’
$S$ is a surface, closed in $\mathbb{R}^3$ oriented out
$$ \iint \vec{F} \cdot d\vec{S} = \iiint\limits_{E} \div F \ \ dV$$
$E$ is a solid in the interior of $S$